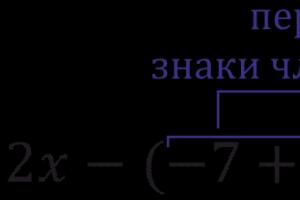Квадратичные формы

Квадратичной формой f(х 1 , х 2 ,...,х n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом: f(х 1 , х 2 ,...,х n) = (a ij = a ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическая матрица (т.е. матрица, симметричная относительно главной диагонали, a ij = a ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где

В самом деле

Например, запишем в матричном виде квадратичную форму .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому

Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма
f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А * = C T AC.

Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формы f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .

Квадратичная форма называется канонической (имеет канонический вид ), если все ее коэффициенты a ij = 0 при i ≠ j, т.е.
f(х 1 , х 2 ,...,х n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .

Ее матрица является диагональной.

Теорема (доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Например, приведем к каноническому виду квадратичную форму
f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 .

Для этого вначале выделим полный квадрат при переменной х 1:

f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 – х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 – х 2 х 3 .

Теперь выделяем полный квадрат при переменной х 2:

f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 – 5(х 2 2 – 2* х 2 *(1/10)х 3 + (1/100)х 3 2) - (5/100)х 3 2 =
= 2(x 1 + х 2) 2 – 5(х 2 – (1/10)х 3) 2 - (1/20)х 3 2 .

Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 , y 2 = х 2 – (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому виду f(y 1 , y 2 , y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют законом инерции квадратичных форм .

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2:
f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 = -3х 2 2 – х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 –
- 2* х 2 ((1/6) х 3 + (2/3)х 1) +((1/6) х 3 + (2/3)х 1) 2) – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 =
= -3(х 2 – (1/6) х 3 - (2/3)х 1) 2 – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 = f(y 1 , y 2 , y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2 , где y 1 = - (2/3)х 1 + х 2 – (1/6) х 3 , y 2 = (2/3)х 1 + (1/6) х 3 и y 3 = x 1 . Здесь положительный коэффициент 2 при y 3 и два отрицательных коэффициента (-3) при y 1 и y 2 (а при использовании другого способа мы получили положительный коэффициент 2 при y 1 и два отрицательных – (-5) при y 2 и (-1/20) при y 3).

Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы , равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичную форму f(X) называют положительно (отрицательно ) определенной , если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е. f(X) > 0 (отрицательна, т.е.
f(X) < 0).

Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная форма f 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в виде f 2 (X) = -(x 1 - х 2) 2 .

В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).

Теорема . Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).

Теорема (критерий Сильвестра) . Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.

Главным (угловым) минором k-го порядка матрицы А n-го порядка называют определитель матрицы, составленный из первых k строк и столбцов матрицы А ().

Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.

Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 .

= (2 - l)*
*(3 - l) – 4 = (6 - 2l - 3l + l 2) – 4 = l 2 - 5l + 2 = 0; D = 25 – 8 = 17;
. Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (-2 - l)*
*(-3 - l) – 4 = (6 + 2l + 3l + l 2) – 4 = l 2 + 5l + 2 = 0; D = 25 – 8 = 17;
. Следовательно, квадратичная форма – отрицательно определенная.

В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где

В самом деле

Например, запишем в матричном виде квадратичную форму .

Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) =Y T (C T AC)Y.

Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формыf(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .

Квадратичная форма называется канонической (имеетканонический вид ), если все ее коэффициентыa ij = 0 приi≠j, т.е.f(х 1 , х 2 ,...,х n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .

Ее матрица является диагональной.

Например, приведем к каноническому виду квадратичную форму f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 .

Для этого вначале выделим полный квадрат при переменной х 1:

f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 – х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 – х 2 х 3 .

Теперь выделяем полный квадрат при переменной х 2:

f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 – 5(х 2 2 – 2* х 2 *(1/10)х 3 + (1/100)х 3 2) - (5/100)х 3 2 = = 2(x 1 + х 2) 2 – 5(х 2 – (1/10)х 3) 2 - (1/20)х 3 2 .

Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 ,y 2 = х 2 – (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому видуf(y 1 ,y 2 ,y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами 1). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называютзаконом инерции квадратичных форм .

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2:f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 = -3х 2 2 – х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 – - 2* х 2 ((1/6) х 3 + (2/3)х 1) +((1/6) х 3 + (2/3)х 1) 2) – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 = = -3(х 2 – (1/6) х 3 - (2/3)х 1) 2 – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 =f(y 1 ,y 2 ,y 3) = -3y 1 2 - -3y 2 2 + 2y 3 2 , гдеy 1 = - (2/3)х 1 + х 2 – (1/6) х 3 ,y 2 = (2/3)х 1 + (1/6) х 3 и y 3 = x 1 . Здесь положительный коэффициент 2 приy 3 и два отрицательных коэффициента (-3) приy 1 иy 2 (а при использовании другого способа мы получили положительный коэффициент 2 приy 1 и два отрицательных – (-5) приy 2 и (-1/20) приy 3).

Квадратичную форму f(X) называютположительно (отрицательно )определенной , если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).

Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в видеf 2 (X) = -(x 1 - х 2) 2 .

Главным (угловым) минором k-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().

Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 .

= (2 -)* *(3 -) – 4 = (6 - 2- 3+ 2) – 4 = 2 - 5+ 2 = 0;D= 25 – 8 = 17; . Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = 2 > 0. Главный минор второго порядка 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+ 2) – 4 = 2 + 5+ 2 = 0;D= 25 – 8 = 17; . Следовательно, квадратичная форма – отрицательно определенная.

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = = -2 < 0. Главный минор второго порядка 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).

И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (2 -)* *(-3 -) – 4 = (-6 - 2+ 3+ 2) – 4 = 2 +- 10 = 0;D= 1 + 40 = 41; . Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = 2 > 0. Главный минор второго порядка 2 = = -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).

1Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пустьf(х 1 , х 2) = 2x 1 х 2 = x 1 2 + 2x 1 х 2 + х 2 2 - x 1 2 - х 2 2 =

= (x 1 + х 2) 2 - x 1 2 - х 2 2 = (x 1 + х 2) 2 – (x 1 2 - 2x 1 х 2 + х 2 2) - 2x 1 х 2 = (x 1 + х 2) 2 – - (x 1 - х 2) 2 - 2x 1 х 2 ; 4x 1 х 2 = (x 1 + х 2) 2 – (x 1 - х 2) 2 ;f(х 1 , х 2) = 2x 1 х 2 = (1/2)* *(x 1 + х 2) 2 – (1/2)*(x 1 - х 2) 2 =f(y 1 ,y 2) = (1/2)y 1 2 – (1/2)y 2 2 , гдеy 1 = х 1 + х 2 , аy 2 = х 1 – х 2 .

Понятие квадратичной формы. Матрица квадратичной формы. Канонический вид квадратичной формы. Метод Лагранжа. Нормальный вид квадратичной формы. Ранг, индекс и сигнатура квадратичной формы. Положительно определенная квадратичная форма. Квадрики.

Понятие квадратичной формы: функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Квадратичной формой от n неизвестных называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных.

Матрица квадратичной формы: Матрицу называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть .

Написать матрицу квадратичной формы:

Следовательно,

В векторно-матричной форме квадратичная форма имеет вид:

A , где

Канонический вид квадратичной формы: Квадратичная форма называется канонической, если все т. е.

Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

Метод Лагранжа : последовательное выделение полных квадратов. Например, если

Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем

Нормальный вид квадратичной формы: Нормальной квадратичной формой называется такая каноническая квадратичная форма, у которой все коэффициенты равны +1 или -1.

Ранг, индекс и сигнатура квадратичной формы: Рангом квадратичной формы А называется ранг матрицы А . Ранг квадратичной формы не изменяется при невырожденных преобразованиях неизвестных.

Количество отрицательных коэффициентов - называется отрицательным индексом формы.

Число положительных членов в каноническом виде называется положительным индексом инерции квадратичной формы, число отрицательных членов - отрицательным индексом. Разность между положительным и отрицательным индексами называетсясигнатурой квадратичной формы

Положительно определенная квадратичная форма: Вещественная квадратичная форма называется положительно определенной (отрицательно определенной), если при любых не равных одновременно нулю вещественных значениях переменных

. (36)

В этом случае матрица также называется положительно определенной (отрицательно определенной).

Класс положительно определенных (отрицательно определенных) форм является частью класса неотрицательных (соответственно неположительных) форм.

Квадрики: Квадрик — n -мерная гиперповерхность в n +1-мерном пространстве, заданная как множество нулей многочлена второй степени. Если ввести координаты {x 1 , x 2 , x n +1 } (в евклидовом или аффинном пространстве), общее уравнение квадрики имеет вид

Это уравнение можно переписать более компактно в матричных обозначениях:

где x = {x 1 , x 2 , x n +1 } — вектор-строка, x T — транспонированный вектор, Q — матрица размера (n +1)×(n +1) (предполагается, что хотя бы один её элемент ненулевой), P — вектор-строка, а R — константа. Наиболее часто рассматривают квадрики над действительнымиили комплексными числами. Определение можно распространить на квадрики в проективном пространстве, см. ниже.

Более общо, множество нулей системы полиномиальных уравнений известно как алгебраическое многообразие. Таким образом, квадрика является (аффинным или проективным) алгебраическим многообразием второй степени и коразмерности 1.

Преобразования плоскости и пространства.

Определение преобразования плоскости. Определение движения. свойства движения. Два вида движений: движение I рода и движение II рода. Примеры движений. Аналитическое выражение движения. Классификация движений плоскости (в зависимости от наличия неподвижных точек и инвариантных прямых). Группа движений плоскости.

Определение преобразования плоскости: Определение. Преобразование плоскости сохраняющее расстояние между точками называется движением (или перемещением) плоскости. Преобразование плоскости называется аффинным , если оно любые три точки, лежащие на одной прямой переводит в три точки также лежащие на одной прямой и при этом сохраняет простое отношение трех точек.

Определение движения: это преобразования фигур, при котором сохраняются расстояния между точками. Если две фигуры точно совместить друг с другом посредством движения, то эти фигуры одинаковы, равны.

Свойства движения: всякое сохраняющее ориентацию движение плоскости является либо параллельным переносом, либо поворотом, всякое меняющее ориентацию движение плоскости является либо осевой симметрией, либо скользящей симметрией. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения. При движении сохраняются углы между полупрямыми.

Два вида движений: движение I рода и движение II рода: Движения первого рода - такие движения, которые сохраняют ориентацию базисов некоей фигуры. Они могут быть реализованы непрерывными движениями.

Движения второго рода - такие движения, которые изменяют ориентацию базисов на противоположную. Они не могут быть реализованы непрерывными движениями.

Примерами движений первого рода являются перенос и поворот вокруг прямой, а движениями второго рода - центральная и зеркальная симметрии.

Композицией любого числа движений первого рода является движение первого рода.

Композиция четного числа движений второго рода есть движение 1 рода, а композиция нечетного числа движений 2 рода - движение 2 рода.

Примеры движений: Параллельный перенос . Пусть а — данный вектор. Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в точку М 1 , что вектор MМ 1 равен вектору а.

Параллельный перенос является движением, поскольку представляет собой отображение плоскости на себя, сохраняющее расстояния. Наглядно это движение можно представить как сдвиг всей плоскости в направлении данного вектора а на его длину.

Поворот . Обозначим на плоскости точку О (центр поворота ) и зададим угол α (угол поворота ). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в точку М 1 , что ОМ = ОМ 1 и угол MOМ 1 равен α. При этом точка О остается на своем месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одинаковом направлении — по часовой стрелке или против часовой стрелки (на рисунке изображен поворот против часовой стрелки).

Поворот является движением, поскольку представляет собой отображение плоскости на себя, при котором сохраняются расстояния.

Аналитическое выражение движения: аналитическая связь, между координатами прообраза и образа точки имеет вид (1).

Классификация движений плоскости (в зависимости от наличия неподвижных точек и инвариантных прямых): Определение:

Точка плоскости инвариантной (неподвижной), если при данном преобразовании она переходит в себя.

Пример: При центральной симметрии инвариантной является точка центра симметрии. При повороте инвариантной является точка центра поворота. При осевой симметрии инвариантной является прямая — ось симметрии — это прямая инвариантных точек.

Теорема: Если движение не имеет ни одной инвариантной точки, то оно имеет хотя бы одно инвариантное направление.

Пример: Параллельный перенос. Действительно, прямые, параллельные этому направлению инвариантных как фигура в целом, хотя не состоит из инвариантных точек.

Теорема: Если движется какой-то луч, луч переводит в себя, то это движение либо тождественное преобразование, либо симметрия относительно прямой содержащей данный луч.

Поэтому по наличию инвариантных точек или фигур можно провести классификацию движений.

Название движения	Инвариантные точки	Инвариантные прямые
Движение I рода.
1. - поворота	(центр) - 0	нет
2. Тождественное преобразование	все точки плоскости	все прямые
3. Центральная симметрия	точка 0 - центр	все прямые, проходящие через точку 0
4. Параллельный перенос	нет	все прямые
Движение II рода.
5. Осевая симметрия.	множество точек	ось симметрии (прямая ) все прямые

Группа движений плоскости: В геометрии важную роль играют группы самосовмещений фигур. Если - некоторая фигура на плоскости (или в пространстве), то можно рассмотреть множество всех тех движений плоскости (или пространства), при которых фигура переходит в себя.

Это множество является группой. Например, для равностороннего треугольника группа движений плоскости, переводящих треугольник в себя, состоит из 6 элементов: поворотов на углы вокруг точки и симметрий относительно трех прямых.

Они изображены на рис. 1 красными линиями. Элементы группы самосовмещений правильного треугольника могут быть заданы и иначе. Чтобы пояснить это, пронумеруем вершины правильного треугольника числами 1, 2, 3. Любое самосовмещение треугольника переводит точки 1, 2, 3 в те же самые точки, но взятые в ином порядке, т.е. может быть условно вписано в виде одной из таких скобок:

и т.д.

где числами 1, 2, 3 обозначены номера тех вершин, в которые переходят вершины 1, 2, 3 в результате рассматриваемого движения.

Проективные пространства и их модели .

Понятие проективного пространства и модели проективного пространства. Основные факты проективной геометрии. Связка прямых с центром в точке O - модель проективной плоскости . Проективные точки. Расширенная плоскость - модель проективной плоскости. Расширенное трехмерное аффинное или евклидово пространство - модель проективного пространства . Изображения плоских и пространственных фигур при параллельном проектировании.

Понятие проективного пространства и модели проективного пространства:

Проективное пространство над полем — пространство, состоящее из прямых (одномерных подпространств) некотороголинейного пространства над данным полем. Прямые пространства называются точками проективного пространства. Это определение поддаётся обобщению на произвольное тело

Если имеет размерность , то размерностью проективного пространства называется число , а само проективное пространство обозначается и называется ассоциированным с (чтобы это указать, принято обозначение ).

Переход от векторного пространства размерности к соответствующему проективному пространству называется проективизацией пространства .

Точки можно описывать с помощью однородных координат.

Основные факты проективной геометрии: Проективная геометрия — раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции. Проективная геометрия может изучаться как с чисто геометрической точки зрения, так с аналитической (с помощью однородных координат) и салгебраической, рассматривая проективную плоскость как структуру над полем. Часто, и исторически, вещественная проективная плоскость рассматривается как Евклидова плоскость с добавлением «прямой в бесконечности».

Тогда как свойства фигур, с которыми имеет дело Евклидова геометрия, являются метрическими (конкретные величины углов, отрезков, площадей), а эквивалентность фигур равнозначна их конгруэнтности (т.е. когда фигуры могут быть переведены одна в другую посредством движения с сохранением метрических свойств), существуют более "глубоко лежащие" свойства геометрических фигур, которые сохраняются при преобразованиях более общего типа, чем движение. Проективная геометрия занимается изучением свойств фигур, инвариатных при классе проективных преобразований , а также самих этих преобразований.

Проективная геометрия дополняет Евклидову, предоставляя красивые и простые решения для многих задач, осложнённых присутствием параллельных прямых. Особенно проста и изящна проективная теория конических сечений.

Есть три главных подхода к проективной геометрии: независимая аксиоматизация, дополнение Евклидовой геометрии , и структура над полем.

Аксиоматизация

Проективное пространство можно определить с помощью разного набора аксиом.

Коксетер предоставляет следующие:

1. Существует прямая и точка не на ней.

2. На каждой прямой есть по крайней мере три точки.

3. Через две точки можно провести ровно одну прямую.

4. Если A , B , C , и D — различные точки и AB и CD пересекаются, то AC и BD пересекаются.

5. Если ABC — плоскость, то существует по крайней мере одна точка не в плоскости ABC .

6. Две различные плоскости пересекаются по крайней мере в двух точках.

7. Три диагональные точки полного четырёхугольника не коллинеарны.

8. Если три точки на прямой X X

Проективная плоскость (без третьего измерения) определяется несколько другими аксиомами:

1. Через две точки можно провести ровно одну прямую.

2. Любые две прямые пересекаются.

3. Существует четыре точки, из которых нет трёх коллинеарных.

4. Три диагональные точки полных четырёхугольников не коллинеарны.

5. Если три точки на прямой X инвариантны по отношению к проективности φ, то все точки на X инвариантны по отношению к φ.

6. Теорема Дезарга : Если два треугольника перспективны сквозь точку, то они перспективны сквозь прямую.

При наличии третьего измерения, теорема Дезарга может быть доказана без введения идеальных точки и прямой.

Расширенная плоскость - модель проективной плоскости: возьмем в аффинном простран- стве A3 связку прямых S(O) с центром в точке O и плоскость Π, не проходя- щую через центр связки: O 6∈ Π. Связка прямых в аффинном пространстве является моделью проективной плоскости. Зададим отображение множества точек плоскости Π на множество прямых связки S (Бля, молись если достался этот вопрос, прости)

Расширенное трехмерное аффинное или евклидово пространство - модель проективного пространства :

Для того, чтобы сделать отображение сюръективным, повторим процесс формального расширения аффинной плоскости Π до плоскости проективной, Π, дополняя плоскость Π множеством несобственных точек {M∞} таким, что: ({M∞}) = P0(O). Поскольку в отображении прообразом каждой плоскости связки плоскостей S(O) является прямая на плоскости d, то очевидно, что множество всех несобственных точек расширенной плоскости: Π = Π ∩ {M∞}, {M∞}, представляет собой несобственную прямую d∞ расширенной плос- кости, являющуюся прообразом особой плоскости Π0: (d∞) = P0(O) (= Π0). (I.23) Договоримся, что последнее равенство P0(O) = Π0 здесь и в дальнейшем мы будем понимать в смысле равенства множеств точек, но наделенных раз- личной структурой. Дополнив аффинную плоскость несобственной прямой, мы добились того, что отображение (I.21) стало биективным на множестве всех точек расширенной плоскости:

Изображения плоских и пространственных фигур при параллельном проектировании:

В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование. Пусть p - некоторая плоскость, l - пересекающая ее прямая (рис. 1). Через произвольную точку A , не принадлежащую прямой l , проведем прямую, параллельную прямой l . Точка пересечения этой прямой с плоскостью p называется параллельной проекцией точки A на плоскость p в направлении прямой l . Обозначим ее A ". Если точка A принадлежит прямой l , то параллельной проекцией A на плоскость p считается точка пересечения прямой l с плоскостью p.

Таким образом, каждой точке A пространства сопоставляется ее проекция A " на плоскость p. Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l.

Группа проективных преобразований. Приложение к решению задач.

Понятие проективного преобразования плоскости. Примеры проективных преобразований плоскости. Свойства проективных преобразований. Гомология, свойства гомологии. Группа проективных преобразований.

Понятие проективного преобразования плоскости: Понятие проективного преобразования обобщает понятие центральной проекции. Если выполнить центральную проекцию плоскости α на некоторую плоскость α 1 , затем проекцию α 1 на α 2 , α 2 на α 3 , … и, наконец, какой-то плоскости α n опять на α 1 , то композиция всех этих проекций и есть проективное преобразование плоскости α; в такую цепочку можно включить ипараллельные проекции.

Примеры проективных преобразований плоскости: Проективным преобразованием пополненной плоскости называется ее взаимно-однозначное отображение на себя, при котором сохраняется коллинеарность точек, или, другими словами, образом любой прямой является прямая. Всякое проективное преобразование есть композиция цепочки центральных и параллельных проекций. Аффинное преобразование - это частный случай проективного, при котором бесконечно удаленная прямая переходит сама в себя.

Свойства проективных преобразований:

При проективном преобразовании три точки не лежащие на прямой переходят в три точки не лежащие на прямой.

При проективном преобразовании репер переходит в репер.

При проективном преобразовании прямая переходит в прямую, пучок переходит в пучок.

Гомология, свойства гомологии:

Проективное преобразование плоскости, которое имеет прямую инвариантных точек, а значит, и пучок инвариантных прямых называется гомологией.

1. Прямая, проходящая через несовпадающие соответственные точки гомологии, является инвариантной прямой;

2. Прямые, проходящие через несовпадающие соответственные точки гомологии, принадлежат одному пучку, центр которого является инвариантной точкой.

3. Точка, ее образ и центр гомологии лежат на одной прямой.

Группа проективных преобразований: рассмотрим проективное отображение проективной плоскости P 2 на себя, то есть проективное преобразование этой плоскости (P 2 ’ = P 2).

Как и прежде композицией f проективных преобразований f 1 и f 2 проективной плоскости P 2 назовем результат последовательного выполнения преобразований f 1 и f 2: f = f 2 °f 1 .

Теорема 1: множество H всех проективных преобразований проективной плоскости P 2 является группой относительно композиции проективных преобразований.

Квадратичной формой называется однородный многочлен 2-й степени от нескольких переменных.

Квадратичная форма от переменных состоит из слагаемых двух типов: квадратов переменных и их попарных произведений с некоторыми коэффициентами. Квадратичную форму принято записывать в виде следующей квадратной схемы:

Пары подобных членов записываются с одинаковыми коэффициентами, так что каждый из них составляет половину коэффициента при соответствующем произведении переменных. Таким образом, каждая квадратичная форма естественным образом связывается с матрицей ее коэффициентов, которая является симметричной.

Квадратичную форму удобно представлять и в следующей матричной записи. Обозначим через X столбец из переменных через X - строку т. е. матрицу, транспонированную с X. Тогда

Квадратичные формы встречаются во многих разделах математики и ее приложений.

В теории чисел и кристаллографии рассматриваются квадратичные формы в предположении, что переменные принимают только целочисленные значения. В аналитической геометрии квадратичная форма входит в состав уравнения кривой (или поверхности) порядка. В механике и физике квадратичная форма появляется для выражения кинетической энергии системы через компоненты обобщенных скоростей и т. д. Но, кроме того, изучение квадратичных форм необходимо и в анализе при изучении функций от многих переменных, в вопросах, для решения которых важно выяснить, как данная функция в окрестности данной точки отклоняется от приближающей ее линейной функции. Примером задачи этого типа является исследование функции на максимум и минимум.

Рассмотрим, например, задачу об исследовании на максимум и минимум для функции от двух переменных имеющей непрерывные частные производные до порядка. Необходимым условием для того, чтобы точка давала максимум или минимум функции является равенство нулю частных производных порядка в точке Допустим, что это условие выполнено. Придадим переменным х и у малые приращения и к и рассмотрим соответствующее приращение функции Согласно формуле Тейлора это приращение с точностью до малых высших порядков равно квадратичной форме где - значения вторых производных вычисленные в точке Если эта квадратичная форма положительна при всех значениях и к (кроме ), то функция имеет минимум в точке если отрицательна, то - максимум. Наконец, если форма принимает и положительные и отрицательные значения, то не будет ни максимума, ни минимума. Аналогичным образом исследуются и функции от большего числа переменных.

Изучение квадратичных форм в основном заключается в исследовании проблемы эквивалентности форм относительно той или другой совокупности линейных преобразований переменных. Две квадратичные формы называются эквивалентными, если одна из них может быть переведена в другую посредством одного из преобразований данной совокупности. С проблемой эквивалентности тесно связана проблема приведения формы, т. о. преобразования ее к некоторому возможно простейшему виду.

В различных вопросах, связанных с квадратичными формами, рассматриваются и различные совокупности допустимых преобразований переменных.

В вопросах анализа применяются любые неособенные преобразования переменных; для целей аналитической геометрии наибольший интерес представляют ортогональные преобразования, т. е. те, которым соответствует переход от одной системы переменных декартовых координат к другой. Наконец, в теории чисел и в кристаллографии рассматриваются линейные преобразования с целыми коэффициентами и с определителем, равным единице.

Мы рассмотрим из этих задач две: вопрос о приведении квадратичной формы К простейшему виду посредством любых неособенных преобразований и тот же вопрос для преобразований ортогональных. Прежде всего выясним, как преобразуется матрица квадратичной формы при линейном преобразовании переменных.

Пусть , где А - симметричная матрица из коэффициентов формы, X - столбец из переменных.

Сделаем линейное преобразование переменных, записав его сокращенно . Здесь С обозначает матрицу коэффициентов этого преобразования, X - столбец из новых переменных. Тогда и, следовательно, так что матрицей преобразованной квадратичной формы является

Матрица автоматически оказывается симметричной, что легко проверяется. Таким образом, задача о приведении квадратичной формы к простейшему виду равносильна задаче о приведении к простейшему виду симметричной матрицы посредством умножения ее слева и справа на взаимно транспонированные матрицы.

Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра

Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась:)

Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную . Линейной формой переменных называют однородный многочлен 1-й степени:

– какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля) , а – переменные, которые могут принимать произвольные значения.

* В рамках данной темы будем рассматривать только действительные числа .

С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений , и в данном случае он подразумевает, что у многочлена нет приплюсованной константы .

Например: – линейная форма двух переменных

Теперь форма квадратичная. Квадратичной формой переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных имеет следующий вид:

Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
– в этом слагаемом находится произведение и (квадрат);
– здесь произведение ;
– и здесь произведение .

– сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому:

Иногда встречается «школьный» вариант оформления в духе , но то лишь иногда. Кстати, заметьте, что константы нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.

И квадратичная форма трёх переменных содержит уже шесть членов:

…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.

Однако общую формулу запишем, её удобно оформить «простынёй»:

– внимательно изучаем каждую строчку – ничего страшного тут нет!

Квадратичная форма содержит слагаемых с квадратами переменных и слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний ) . Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).

Матричная запись квадратичной формы

В зависимости от значений рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы – если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений ).

Такая форма называется знакопеременной . И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:

Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной .

А может и не быть:

– всегда, если только одновременно не равны нулю.

– для любого вектора , кроме нулевого .

И вообще, если для любого ненулевого вектора , , то квадратичную форму называют положительно определённой ; если же – то отрицательно определённой .

И всё бы было хорошо, но определённость квадратичной формы виднА лишь в простых примерах, и эта видимость теряется уже при небольшом усложнении:
– ?

Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения , при которых она меньше нуля?

На этот счёт существует теорема : если ВСЕ собственные числа матрицы квадратичной формы положительны* , то она определена положительно. Если все отрицательны – то отрицательно.

* В теории доказано, что все собственные числа действительной симметрической матрицы действительны

Запишем матрицу вышеприведённой формы:
и из уравнения найдём её собственные значения :

Решаем старое доброе квадратное уравнение :

, значит, форма определена положительно, т.е. при любых ненулевых значениях она больше нуля.

Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.

Как быть? Существует более простой путь!

Критерий Сильвестра

Нет, не Сильвестра Сталлоне:) Сначала напомню, что такое угловые миноры матрицы. Это определители которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.

Теперь, собственно, критерий :

1) Квадратичная форма определена положительно тогда и только тогда, когда ВСЕ её угловые миноры больше нуля: .

2) Квадратичная форма определена отрицательно тогда и только тогда, когда её угловые миноры знакочередуются, при этом 1-й минор меньше нуля: , , если – чётное или , если – нечётное.

Если хотя бы один угловой минор противоположного знака, то форма знакопеременна . Если угловые миноры «того» знака, но среди них есть нулевые, то это особый случай, который я разберу чуть позже, после того, как мы перещёлкаем более распространённые примеры.

Проанализируем угловые миноры матрицы :

И это сразу говорит нам о том, что форма не определена отрицательно.

Вывод : все угловые миноры больше нуля, значит, форма определена положительно.

Есть разница с методом собственных чисел? ;)

Запишем матрицу формы из Примера 1 :

первый её угловой минор , а второй , откуда следует, что форма знакопеременна, т.е. в зависимости от значений , может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.

Возьмём форму и её матрицу из Примера 2 :

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём:
, следовательно, форма точно не отрицательна.

, и точно не положительна (т.к. все угловые миноры должны быть положительными) .

Вывод : форма знакопеременна.

Разминочные примеры для самостоятельного решения:

Пример 4

Исследовать квадратичные формы на знакоопределенность

а)

В этих примерах всё гладко (см. конец урока), но на самом деле для выполнения такого задания критерия Сильвестра может оказаться не достаточно .

Дело в том, что существуют «краевые» случаи, а именно: если для любого ненулевого вектора , то форма определена неотрицательно , если – то неположительно . У этих форм существует ненулевые векторы , при которых .

Здесь можно привести такой «баян»:

Выделяя полный квадрат , сразу видим неотрицательность формы: , причём, она равна нулю и при любом векторе с равными координатами, например: .

«Зеркальный» пример неположительно определённой формы:

и ещё более тривиальный пример:
– здесь форма равна нулю при любом векторе , где – произвольное число.

Как выявить неотрицательность или неположительнось формы?

Для этого нам потребуется понятие главных миноров матрицы. Главный минор – это минор, составленный из элементов, которые стоят на пересечении строк и столбцов с одинаковыми номерами. Так, у матрицы существуют два главных минора 1-го порядка:
(элемент находится на пересечении 1-й строки и 1-го столбца);
(элемент находится на пересечении 2-й строки и 2-го столбца),

и один главный минор 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца.

У матрицы «три на три» главных миноров семь, и тут уже придётся помахать бицепсами:
– три минора 1-го порядка,
три минора 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца;
– составлен из элементов 1-й, 3-й строки и 1-го, 3-го столбца;
– составлен из элементов 2-й, 3-й строки и 2-го, 3-го столбца,
и один минор 3-го порядка:
– составлен из элементов 1-й, 2-й, 3-й строки и 1-го, 2-го и 3-го столбца.
Задание на понимание: записать все главные миноры матрицы .
Сверяемся в конце урока и продолжаем.

Критерий Шварценеггера :

1) Ненулевая* квадратичная форма определена неотрицательно тогда и только тогда, когда ВСЕ её главные миноры неотрицательны (больше либо равны нулю).

* У нулевой (вырожденной) квадратичной формы все коэффициенты равны нулю .

2) Ненулевая квадратичная форма с матрицей определена неположительно тогда и только тогда, когда её:
– главные миноры 1-го порядка неположительны (меньше либо равны нулю);
– главные миноры 2-го порядка неотрицательны ;
– главные миноры 3-го порядка неположительны (пошло чередование);
…
– главный минор -го порядка неположителен , если – нечётное либо неотрицателен , если – чётное.

Если хотя бы один минор противоположного знака, то форма знакопеременна.

Посмотрим, как работает критерий в вышеприведённых примерах:

Составим матрицу формы, и в первую очередь вычислим угловые миноры – а вдруг она определена положительно или отрицательно?

Полученные значения не удовлетворяют критерию Сильвестра, однако второй минор не отрицателен , и это вызывает надобность проверить 2-й критерий (в случае 2-й критерий будет не выполнен автоматически, т.е. сразу делается вывод о знакопеременности формы) .

Главные миноры 1-го порядка:
– положительны,
главный минор 2-го порядка:
– не отрицателен.

Таким образом, ВСЕ главные миноры не отрицательны, значит, форма неотрицательна .

Запишем матрицу формы , для которой, очевидно, не выполнен критерий Сильвестра. Но и противоположных знаков мы тоже не получили (т.к. оба угловых минора равны нулю). Поэтому проверяем выполнение критерия неотрицательности / неположительности. Главные миноры 1-го порядка:
– не положительны,
главный минор 2-го порядка:
– не отрицателен.

Таким образом, по критерию Шварценеггера (пункт 2), форма определена неположительно.

Теперь во всеоружии разберём более занятную задачку:

Пример 5

Исследовать квадратичную форму на знакоопределенность

Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем .

Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры:

третий определитель я раскрою по 3-й строке: